Architectures of Exoplanetary Systems: III. Eccentricity and Mutual Inclination Distributions of AMD–Stable Planetary Systems
Abstract
The angular momentum deficit (AMD) of a planetary system is a measure of its orbital excitation and a predictor of long–term stability. We adopt the AMD-stability criteria to constrain the orbital architectures for exoplanetary systems. Previously, He, Ford, & Ragozzine (2019) showed through forward modelling (SysSim) that the observed multiplicity distribution can be well reproduced by two populations consisting of a low and a high mutual inclination component. Here, we show that a broad distribution of mutual inclinations arising from systems at the AMD–stability limit can also match the observed Kepler population. We show that distributing a planetary system’s maximum AMD amongst its planets results in a multiplicity–dependent distribution of eccentricities and mutual inclinations. Systems with intrinsically more planets have lower median eccentricities and mutual inclinations, and this trend is well described by power–law functions of the intrinsic planet multiplicity ($n$). We also find that intrinsic single planets have higher eccentricities ($\sigma_{e,1} \sim 0.25$) than multi-planet systems, and that the trends with multiplicity appear in the observed distributions of period–normalized transit duration ratios. We show that the observed preferences for planet size orderings and uniform spacings are more extreme than what can be produced by the detection biases of the Kepler mission alone. Finally, we find that for systems with detected transiting planets between 5 and 10d, there is another planet with a greater RV signal ~53% of the time.
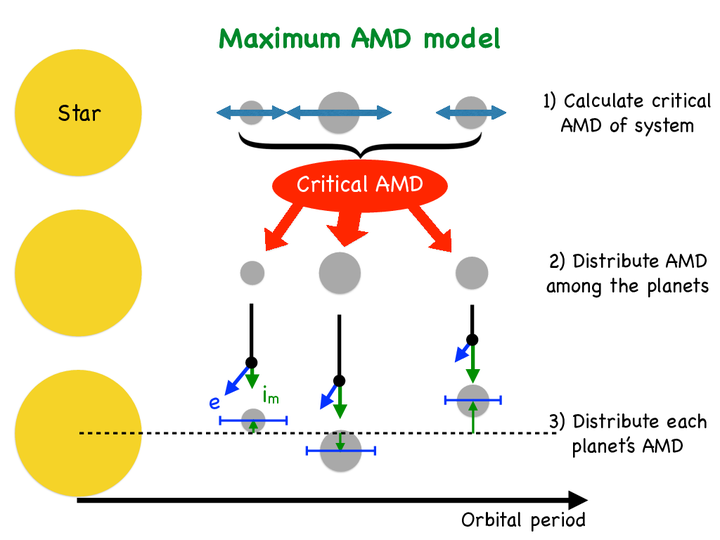
Figure caption: Cartoon illustration of our maximum AMD model. Given a set of planet masses and orbital periods (satisfying our mutual Hill stability criteria for circular orbits) in a system, we first compute the critical AMD of the system in (1) from the collision and MMR overlap conditions. We then distribute the critical AMD amongst the planets, per unit mass, in (2). Finally, we distribute the AMD of each planet amongst their eccentricity and mutual inclination components in (3).