Abstract
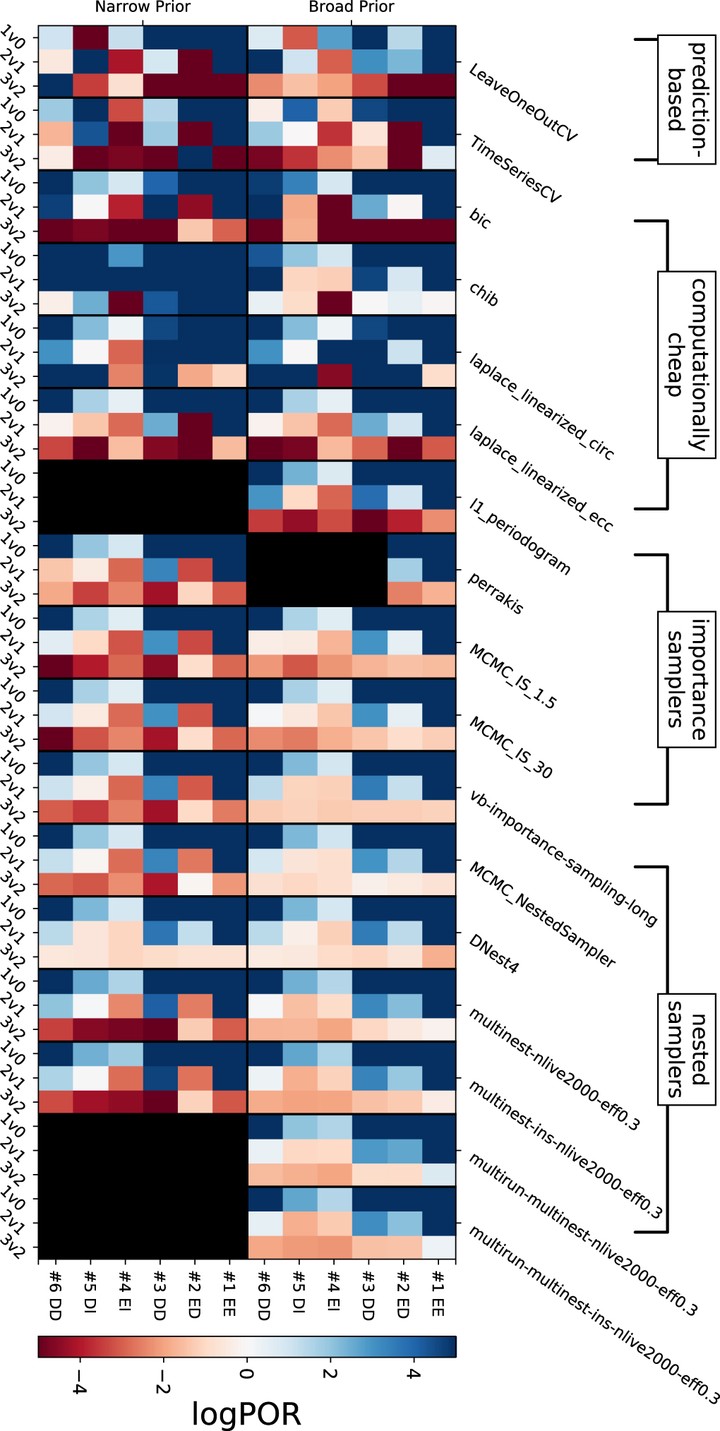
We present results from a data challenge posed to the radial velocity (RV) community: namely, to quantify the Bayesian “evidence” for n={0,1,2,3} planets in a set of synthetically generated RV datasets containing a range of planet signals. Participating teams were provided the same likelihood function and set of priors to use in their analysis. They applied a variety of methods to estimate Z, the marginal likelihood for each n-planet model, including cross-validation, the Laplace approximation, importance sampling, and nested sampling. We found the dispersion in Z across different methods grew with increasing n-planet models: ~3 for 0-planets, ~10 for 1-planet, ~100-1000 for 2-planets, and >10,000 for 3-planets. Most internal estimates of uncertainty in Z for individual methods significantly underestimated the observed dispersion across all methods. Methods that adopted a Monte Carlo approach by comparing estimates from multiple runs yielded plausible uncertainties. Two classes of numerical algorithms (those based on importance and nested samplers) arrived at similar conclusions regarding the ratio of Zs for n and (n+1)-planet models. One analytic method (the Laplace approximation) demonstrated comparable performance. We express both optimism and caution: we demonstrate that it is practical to perform rigorous Bayesian model comparison for <=3-planet models, yet robust planet discoveries require researchers to better understand the uncertainty in Z and its connections to model selection.